cpc

Tokenizers are awkward, but they are unavoidable. It seems very archaic to learn a vocabulary based on frequency in a large text corpus and restrict the model's latent space to decode into this vocab. This abstraction is good most of the time, but starts to fail when models are asked to interact with text the way humans do: incrementally, locally, and at arbitrary character boundaries.

For instance, let's say I am using a model to help edit a small section of this blog post - I select the piece I want to edit, ask a model to suggest a change, and it can replace that text with its enhanced version. Seems simple, until we think about the edge cases. What if the user's start/end selection point is not at a word boundary? What if the user starts typing something else and pauses in the middle of a word to think? These are cases that normal sampling can't handle, but clever tokenizer tricks can help us solve.

An elegant sampling method comes from Cursor Tab. Cursor Tab is a lightweight model that sits inside Cursor that suggests single or multi-step edits based on code that you have already written. It maintains continuity with what you've already written, uses context from the codebase, and suggests a next step that is executed on a tab input. Cursor's problem statement is below.

We want to sample a sequence of tokens $s = (t_1,t_2,...,t_n)$ from a distribution specified by an autoregressive model $p(s)$ given by:

subject to the constraint that s starts with a character prefix $P$, i.e., $P$ is a prefix of repr($t_1$) + repr($t_2$) + ... + repr($t_n$), where + means string concatenation and repr maps a token to the characters it represents. We define $q(s) = p(s | s$ starts with $P)$. It's sufficient to find a way to sample autoregressively from $q(s)$, that is, to sample from $q(t_k|t_1,...,t_{k-1})$ for each $k$.

A huge benefit to open-weights models is the ability to constrain the logits in the decode step. By masking logits we don't care about, we force the model to pick between a small set of tokens, with the softmax applied only on that set. This allows us to steer decoding to match a prefix or a continuation.

What are we sampling from exactly?

It’s worth being precise about what distribution this procedure is actually sampling from. In the ideal case, constrained prefix decoding samples exactly from the conditional distribution $q(s) = p(s \mid s \text{ starts with } P)$, where $p(s)=\prod_k p(t_k \mid t_1,\dots,t_{k-1})$ is the base autoregressive model. The algorithm enforces this constraint incrementally: it keeps track of the portion of the prefix that has not yet been produced, and at each decoding step restricts the model to all and only tokens whose string representations are compatible with that remaining prefix (either by consuming some of it or by completing it outright) before renormalizing and sampling. As long as this allowed token set preserves feasibility (never ruling out a valid continuation and never allowing an invalid one), the procedure is not a heuristic but true conditional sampling. Conceptually, nothing about the model changes; we are simply sampling from the same model under the additional requirement that its decoded output begins with the characters the user has already typed.

Prefix Trie

As we walk backwards through the input text, we want a quick way to determine the breakpoint to start constrained sampling. To do this, we want to check two conditions:

1. There are no tokens that start with the prefix
2. There are no tokens that consume the prefix

We have to build a prefix trie from the vocabulary if we want to do this efficiently. What this means is that we have to build a trie that character-by-character builds up tokens - when you access a prefix in the trie, it tells you all tokens that potentially start with that prefix. You can build this trie once using the entire vocabulary, which makes subsequent steps much faster.

Imagine the vocabulary size is $V$, and the prefix is $P$. To search for all tokens in the vocabulary that start with the prefix $P$ would be $O(VP)$ time, because you need to check all entries of the vocabulary and compare the entries up to length $P$. The trie approach makes this much more efficient. Assume we have a prefix of length $P$ that is broken up character by character in the trie. It will take $O(P)$ time to go through each character in the prefix and make a $O(1)$ access to the trie to see if the node is there as a child of the previous node. Once you reach the last character of the prefix, there is a subtree of size $K$ of all possible token branches stemming from the prefix. It takes $O(P + K)$ time to access all tokens starting with the prefix of length $P$ - in this case, we stop in each token branch when is_word=True (this is a property of each node in the trie). Considering parts of prefixes that are not tokenizable are usually a bit small, this is pretty efficient if we walk backwards in the prefix and determine this breakpoint.

Constrained Sampling

Once we've determined this breakpoint, we need to sample from the language model but constrain the logits to respect the prefix before normal sampling. What this means is the following - imagine we have a sentence "This blog post is so amazi" and the user stopped while typing the rest of the sentence. We determine the breakpoint to be in between "amazi" and "This blog post is so " because we can cleanly tokenize the latter. If we start sampling from the cleanly tokenizable part, then the model could output anything - "This blog post is so cool" or "This blog post is so captivating". However, if the model suggests any of these completions, it overwrites what the user is trying to say. So we need to sample from the language model conditioned on the text after the breakpoint.

1. Find all tokens that start with the prefix remainder.
2. Mask logits corresponding to those tokens.
3. Sample from the language model with the mask
4. Update the prefix remainder if there's still remaining text, and continue the process

Constrained sampling is easy to implement with vLLM, using a LogitsProcessor and creating a callback to update the constrain criteria. In run_cpc.py, we make a callback to update_remaining_prefix in the PrefixConstrainedLogitsProcessor class, which will update the prefix and check if the prefix has been consumed. If the prefix has been consumed, then we sample normally from the model.

CPC Algorithm

The overall algorithm is as follows:

1. Iterate backwards through the prefix $P$ character by character, and check if the remainder can be tokenized or is part of a token. We iterate until we reach a point in which there are no valid token sequences made from the remainder.
2. We set this as a breakpoint and create a mask based on the remainder - the mask consists of masking out tokens that don't start with the remainder or are not part of the remainder.
3. We sample tokens until we pass the remainder and start to sample normally.

In the example below, we sample from the model to determine the completion to a user typing "import tor", with instructions to write a LayerNorm function. We see the model completes the function and its first few tokens overlap with the user's message.

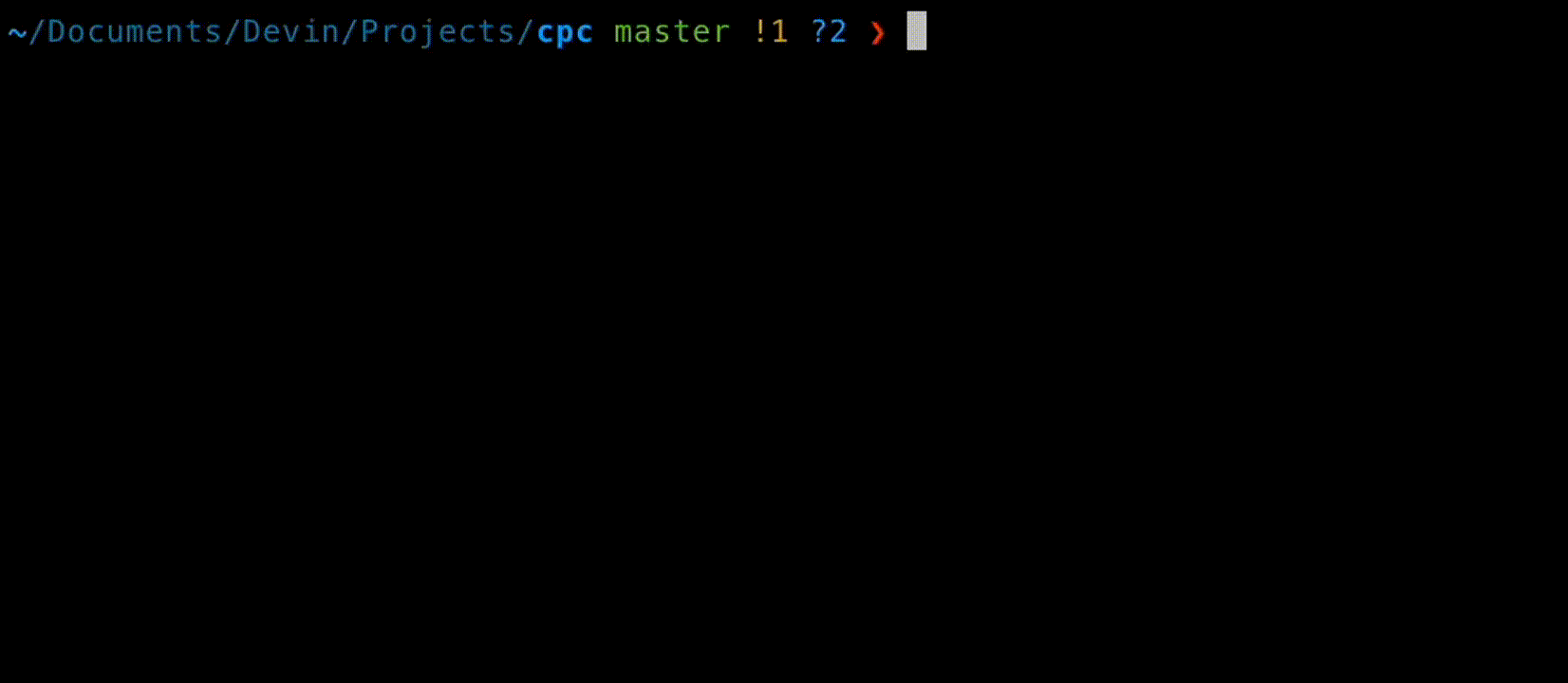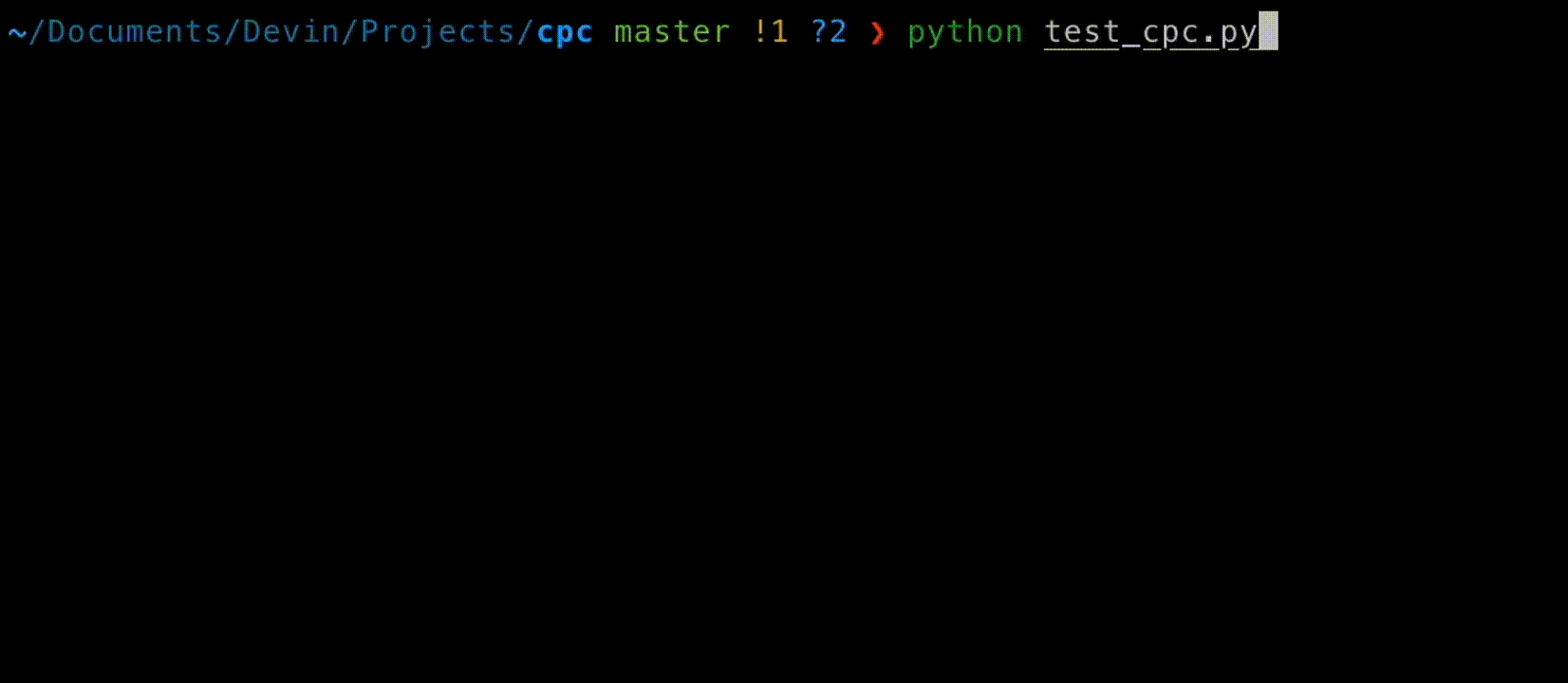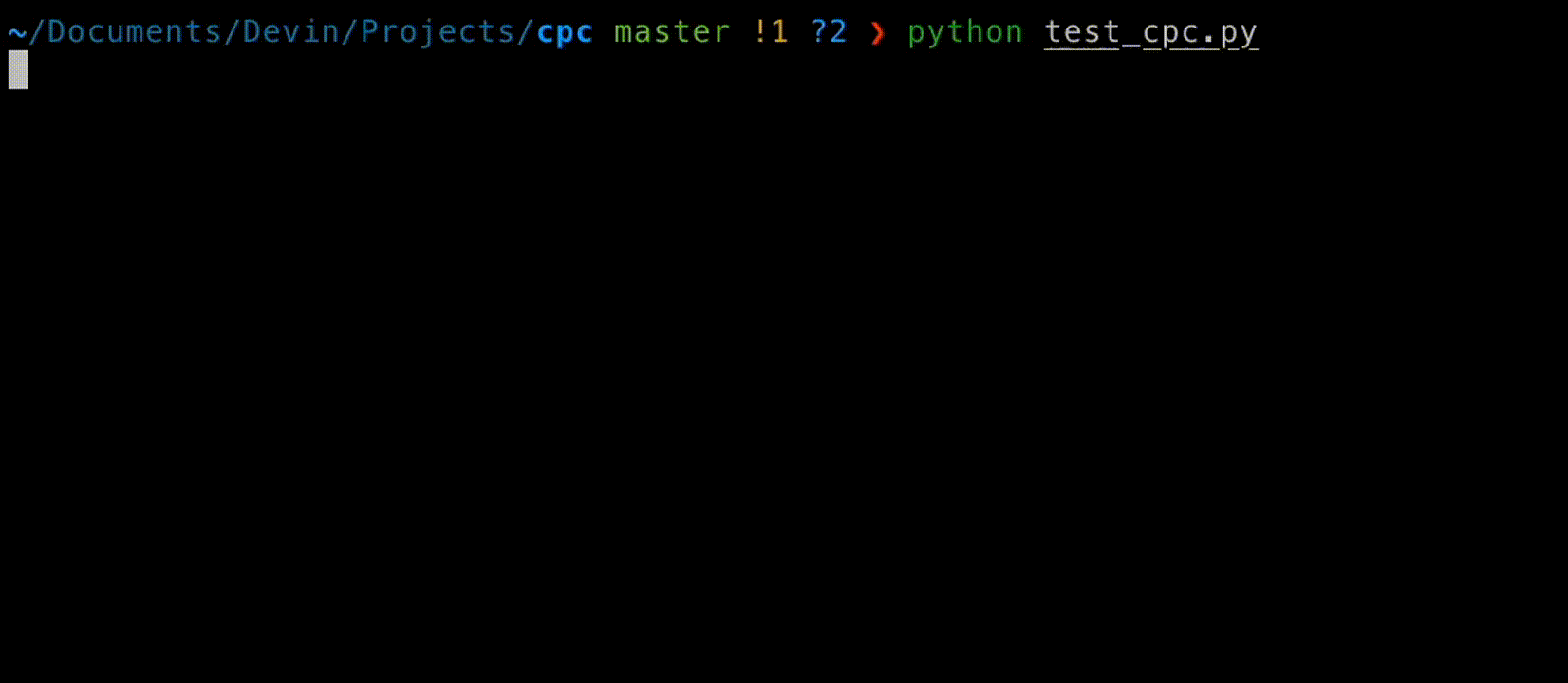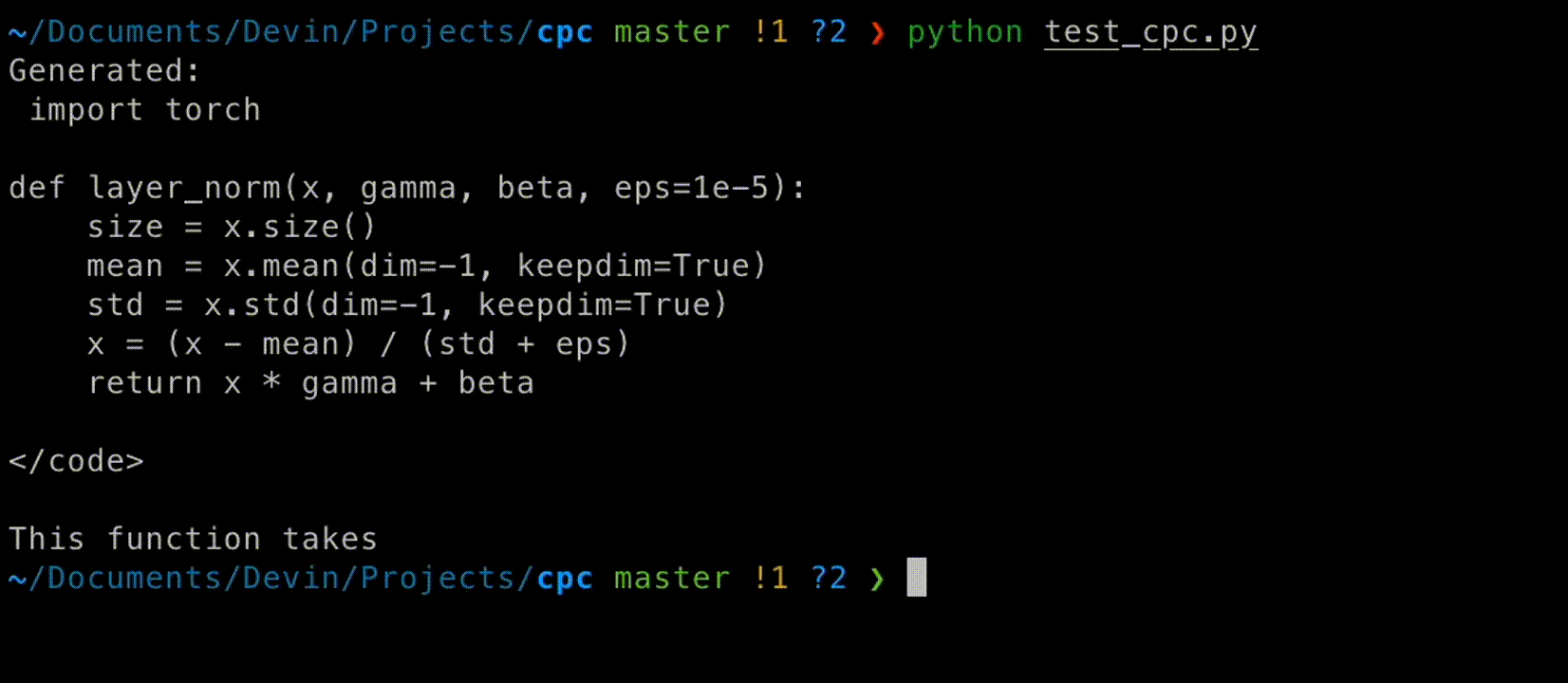
This demo is in no way optimized for a production system. I still see some problems, like strange input token sequences leading to incorrect completions from the model (though this might just be the limit of the model we are running the demo with). I'm sure there's a lot more handling that goes into a system like Cursor Tab, but I've just laid out the primitives.

The code can be found here: https://github.com/dshah3/cpc.

Thanks to my friend Chaitanya Narisetty for brainstorming this solution and post with me.